गॉस का नियम

गॉस का नियम – इस अवसर पर Yuksinau.co.id गॉस लॉ के बारे में सामग्री की समीक्षा करेगा. इस समय की चर्चा में समझ शामिल है, ध्वनि, विद्युत क्षेत्र बल रेखाएँ, सूत्र, विद्युत प्रवाह और उदाहरण की समस्याएं. उसके लिए हम केवल नीचे पूर्ण समीक्षा को देखें.

विषय - सूची

गौस लॉ को समझना

भौतिकी में, गॉस का कानून एक ऐसा कानून है जो उत्पन्न होने वाले विद्युत क्षेत्र के साथ एक विद्युत आवेश के वितरण को जोड़ता है.

गॉस का कानून भौतिक विज्ञानी कार्ल फ्रेडरिक गॉस द्वारा वर्ष का आविष्कार किया गया कानून था 1835, गॉस का कानून मैक्सवेल के समीकरणों में से एक है, मैक्सवेल के समीकरण में शामिल कुछ कानून हैं, फैराडे का इंडक्शन लॉ, गॉस का नियम चुंबकत्व, साथ ही साथ एम्पीयर श्रृंखला के कानून. कोलॉम्ब के कानून को प्राप्त करने के लिए गॉस के अपने कानून का उपयोग किया जा सकता है.

विद्युत प्रवाह से संबंधित नियम ,गॉस कानून के बारे में अधिक विस्तार से चर्चा करने से पहले, आइए, गॉस कानून को बेहतर ढंग से समझने के लिए विद्युत प्रवाह की व्याख्या देखें।. इलेक्ट्रिक फ्लक्स विद्युत बल और उस क्षेत्र के क्षेत्र का उत्पाद है जिसे उस क्षेत्र से पार किया जाता है.

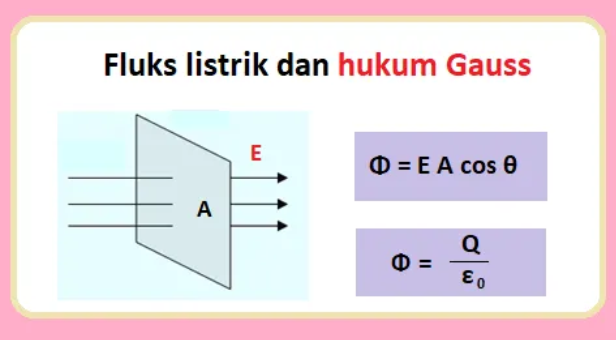
यदि एक सजातीय सजातीय विद्युत क्षेत्र से बल की रेखाएं होती हैं जो क्षेत्र ए के क्षेत्र में प्रवेश करती हैं, तो विद्युत प्रवाह (Φ) एक क्षेत्र से गुजरना विद्युत क्षेत्र की ताकत पर निर्भर करता है, क्षेत्र का क्षेत्र घुस गया, और पतन का कोण. दो संभावनाएँ हैं, यही है, बल लंबवत रूप से गिरता है या बल लंबवत नहीं गिरता है.

जब शैली सीधे गिरती है, निम्नानुसार तैयार किया जा सकता है:

Φ = ई. ए

जब शैली अनियमित रूप से गिरती है, निम्नानुसार तैयार किया जा सकता है:

Φ = ई. ए. क्योंकि θ

जानकारी:
Φ = विद्युत प्रवाह (पश्चिम बंगाल).
ई = विद्युत क्षेत्र की ताकत (एन / सी).
ए = क्षेत्र का क्षेत्र विद्युत क्षेत्र द्वारा प्रवेश किया (एम 2).
θ = सामान्य क्षेत्र रेखा और आवक बल के बीच का कोण.

गॉस का नियम लगता है

गौसियन कानून में निम्नलिखित ध्वनि है:

"एक बंद सतह में प्रवेश करने वाली बल की लाइनों की संख्या सीधे चार्ज के लिए आनुपातिक होती है”.

गॉस के कानून को निम्नानुसार तैयार किया जा सकता है:

Φ = ई. ए. क्योंकि θ = क्यू /ε_o
क्यू = इ. ए. क्योंकि θ

जानकारी:
क्यू = बंद सतह से घिरा हुआ भार
ε 0 = हवा की पारगम्यता

लाइन – विद्युत क्षेत्र बल रेखाएँ.

विद्युत क्षेत्र को काल्पनिक रेखाओं द्वारा दर्शाया जा सकता है जिसकी दिशा धनात्मक आवेश से निकलती है और वह दिशा ऋणात्मक आवेश में प्रवेश करती है. विद्युत लाइनों का घनत्व दर्शाता है कि विद्युत क्षेत्र कितना मजबूत है.

विद्युत क्षेत्र बल रेखाएँ जो एक आयताकार क्षेत्र के लंबवत प्रवेश करती हैं, जिसमें क्षेत्र A है. प्रति यूनिट क्षेत्र में विद्युत क्षेत्र बल लाइनों की संख्या सीधे विद्युत क्षेत्र की ताकत के लिए आनुपातिक है, ताकि क्षेत्र बल रेखाओं का योग एक ऐसे क्षेत्र में प्रवेश करे जिसकी चौड़ाई A की बजाय एक सीधी E.A हो.

एफइलेक्ट्रिक लुक्स

इलेक्ट्रिक फ्लक्स को एक बिजली के क्षेत्र के बीच एक स्केलर गुणन के परिणाम के रूप में परिभाषित किया गया है और एक वेक्टर मजबूत है जो मैदान के बाहर की सतह से एक वेक्टर है।. एक सतह से गुजरने वाले विद्युत प्रवाह को निम्नानुसार तैयार किया जा सकता है:

Φ = ई.ए. = ईए. क्योंकि θ

साथ में :
A सतह क्षेत्र है
θ विद्युत क्षेत्र और सतह क्षेत्र वेक्टर के बीच उत्पादित कोण है.

यदि सतह में प्रवेश किया जाता है, तो क्षेत्र में कई खंड होते हैं,फिर कुल प्रवाह प्रत्येक खंड में कुल प्रवाह के बराबर है. कुल प्रवाह को निम्नानुसार तैयार किया जा सकता है :

Φ = Φ 1+ Φ 2+ Φ 3+ Φ 4+….+ Φ n
Φ = E1.A1 + E2.A2 + E3.A3 + E4.A4 +…+ En.An
Φ = E1.A1cos θ 1+E2.A2cos θ 2+E3.A3cos θ +E3.A3cos θ +E4.A4cos θ +…+En.Ancos θn

जहां E वह क्षेत्र है जो A की सतह पर प्रवेश करता है.

नमूना प्रश्न

प्रश्न 1 : जब एक पक्ष लंबाई के साथ एक वर्ग होता है 30 से। मी, और एक सजातीय विद्युत क्षेत्र 400 एन / सी को आयताकार में एक दिशा में गोली मारी जाती है जो आयताकार विमान के लंबवत है, वर्ग विमान में प्रवेश करने वाले विद्युत प्रवाह की मात्रा की गणना करें?

उत्तर :

मालूम: साइड लंबाई = 30 सेमी
ए = 30 एक्स 30 = 900 सेमी² = 9 एक्स 10^-2 म²
ई = 400 एन / सी

यह पूछने पर : विद्युतीय फ्लक्स (Φ)

उत्तर :
Φ = ई.ए.
Φ = 400.9 x 10^-2 म²
Φ = 36 डब्ल्यूबी

प्रश्न 2 : यदि उंगलियों के साथ एक वृत्त क्षेत्र है 10 से। मी. और एक विद्युत क्षेत्र की ताकत है (इ) बड़े के साथ 300 उस क्षेत्र में जाने वाले एन / सी एक कोण का उत्पादन करते हैं 90⁰ मैदान में. विद्युत प्रवाह की गणना करें?

उत्तर:

मालूम :
ई = 300 एन / सी
उंगलियां = 10 सेमी
θ = 90⁰ = 0

यह पूछने पर:
विद्युतीय फ्लक्स?

उत्तर:
एक = π आर²
एक = 3,14 एक्स 10²
एक = 314 से। मी² = 3,14 एक्स 10^-2

Φ = ई. A.cos θ
Φ = 300 एक्स 3,14 एक्स 10^-2 x कॉस 90
Φ = 300 एक्स 3,14 एक्स 10^-2 एक्स 0
Φ = 0

ऐसी है गॉस लॉ की चर्चा. आशा है कि यह पाठकों के लिए उपयोगी हो सकता है. आप अन्य भौतिकी सामग्रियों के बारे में भी जान सकते हैं जो हमने नीचे दिए हैं.

अन्य लेख :

विद्युत चुम्बकीय तरंग
संभावित ऊर्जा सूत्र
कंडक्टर और आइसोलेटर
लेनज का नियम

The post हुकुम गौस पहली बार दिखाई दी YukSinau.co.id पर.

शिक्षा